6. Underfitting and Overfitting¶
In machine learning we describe the learning of the target function from training data as inductive learning. Induction refers to learning general concepts from specific examples which is exactly the problem that supervised machine learning problems aim to solve. This is different from deduction that is the other way around and seeks to learn specific concepts from general rules.
Generalization refers to how well the concepts learned by a machine learning model apply to specific examples not seen by the model when it was learning. The goal of a good machine learning model is to generalize well from the training data to any data from the problem domain. This allows us to make predictions in the future on data the model has never seen.
There is a terminology used in machine learning when we talk about how well a machine learning model learns and generalizes to new data, namely overfitting and underfitting. Overfitting and underfitting are the two biggest causes for poor performance of machine learning algorithms.
6.1. Overfitting¶
Overfitting refers to a model that models the training data too well. Overfitting happens when a model learns the detail and noise in the training data to the extent that it negatively impacts the performance of the model on new data. This means that the noise or random fluctuations in the training data is picked up and learned as concepts by the model. The problem is that these concepts do not apply to new data and negatively impact the models ability to generalize.
Overfitting is more likely with nonparametric and nonlinear models that have more flexibility when learning a target function. As such, many nonparametric machine learning algorithms also include parameters or techniques to limit and constrain how much detail the model learns.
Overfitting occurs when a statistical model or machine learning algorithm captures the noise of the data. Intuitively, overfitting occurs when the model or the algorithm fits the data too well. Specifically, overfitting occurs if the model or algorithm shows low bias but high variance. Overfitting is often a result of an excessively complicated model, and it can be prevented by fitting multiple models and using validation or cross-validation to compare their predictive accuracies on test data.
6.2. Underfitting¶
Underfitting refers to a model that can neither model the training data nor generalize to new data. An underfit machine learning model is not a suitable model and will be obvious as it will have poor performance on the training data. Underfitting is often not discussed as it is easy to detect given a good performance metric. The remedy is to move on and try alternate machine learning algorithms. Nevertheless, it does provide a good contrast to the problem of overfitting.
Underfitting occurs when a statistical model or machine learning algorithm cannot capture the underlying trend of the data. Intuitively, underfitting occurs when the model or the algorithm does not fit the data well enough. Specifically, underfitting occurs if the model or algorithm shows low variance but high bias. Underfitting is often a result of an excessively simple model.
6.3. Example¶
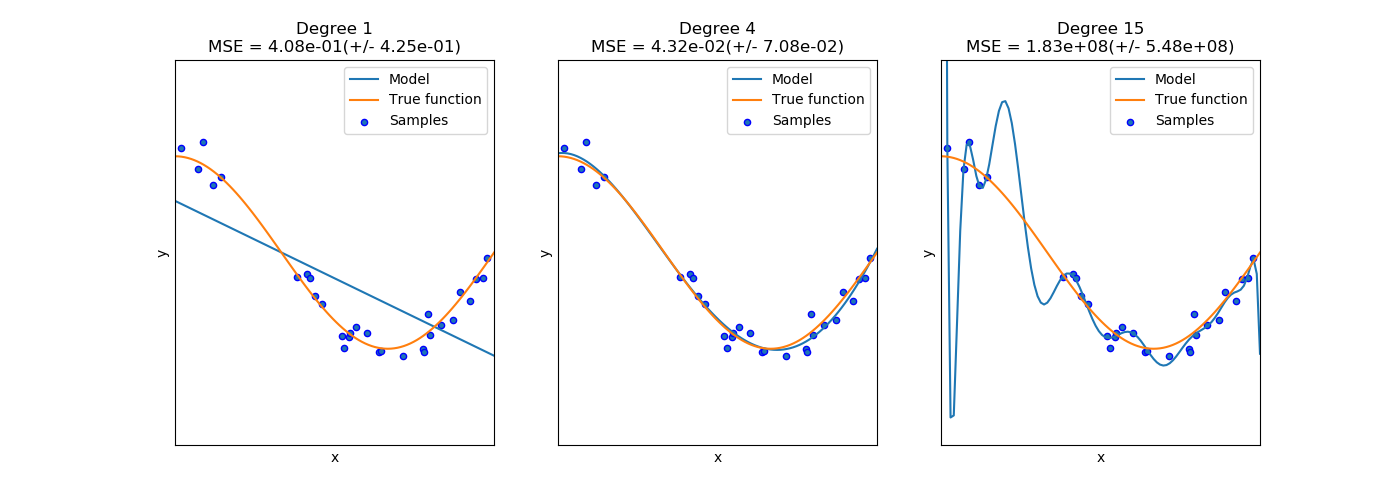
This example demonstrates the problems of underfitting and overfitting and how we can use linear regression with polynomial features to approximate nonlinear functions. The plot shows the function that we want to approximate, which is a part of the cosine function. In addition, the samples from the real function and the approximations of different models are displayed. The models have polynomial features of different degrees. We can see that a linear function (polynomial with degree 1) is not sufficient to fit the training samples. This is called underfitting. A polynomial of degree 4 approximates the true function almost perfectly. However, for higher degrees the model will overfit the training data, i.e. it learns the noise of the training data. We evaluate quantitatively overfitting / underfitting by using cross-validation. We calculate the mean squared error (MSE) on the validation set, the higher, the less likely the model generalizes correctly from the training data.
Citations
Footnotes
References